Բնության մեջ մեխանիկական շարժումները խիստ բազմազան են: Դրանցում իրենց յուրահատկությամբ առանձնանում են տատանողական շարժումները կամ մեխանիկական տատանումնները:
Տատանումները շարժումներ են, որոնք կատարվում են հերթականորեն՝ հակադիր ուղղություններով: Տատանումներն ունեն բնորոշ հատկություն՝ կրկնելիություն:
Այն ամենափոքր ժամանակամիջոցը, որի ընթացքում տատանումները կրկնվում են, կոչվում է տատանման պարբերություն (T) :
Տատանումների պարբերությունը մեկ լրիվ տատանում կատարելու համար անհրաժեշտ ժամանակամիջոցն է։T=tn
Տատանումների պարբերությունը որոշելու համար անհրաժեշտ է t ժամանակը բաժանել այդ ընթացքում կատարված տատանումների n թվի վրա.
Տատանումների պարբերությունը չափվում է ժամանակի միավորներով` վայրկյաններով, րոպեներով և այլն։
Տատանումների հաճախությունը մեկ վայրկյանում կատարվող տատանումների թիվն է։
Ուշադրություն
Միավորների ՄՀ-ում հաճախության չափման միավոր է ընդունված մեկ հերցը (1 Հց)` գերմանացի ֆիզիկոս Հ. Հերցի պատվին (1857−1894 թթ.)։Տատանումների հաճախությունը որոշելու համար անհրաժեշտ է տատանումների n թիվը բաժանել այն ժամանակի վրա, որի ընթացքում այդ տատանումները տեղի են ունեցել` ν=nt
Տատանումների T պարբերության և ν հաճախության համար ճիշտ են այն բոլոր բանաձևերը`
T=1ν և ν=1T
Տատանումների լայնույթն այն առավելագույն հեռավորությունն է, որի չափով իր հավասարակշռության դիրքից կարողանում է հեռանալ տատանվող մարմինը։
Ուշադրություն
Տատանումների լայնույթը չափվում է երկարության միավորներով` մետրով, սանտիմետրով և այլն։
Օրինակ
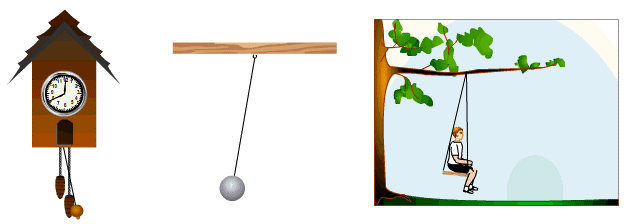
Տատանողական շարժումը դիտարկենք թելավոր և զսպանակավոր ճոճանակների օրինակներով։
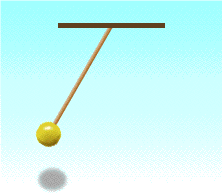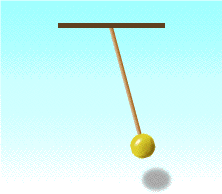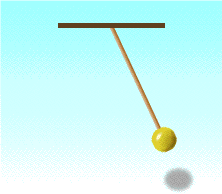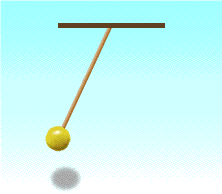
Մաթեմատիկական (թելավոր) ճոճանակը բաղկացած է l երկարությամբ բարակ թեթև թելից, որից կախված m զանգվածով գնդիկը։ Եթե գնդիկը, հավասարակշռության դիրքից հանելով, մի կողմ շեղենք ու բաց թողնենք, այն կսկսի տատանվել, այսինքն կրկնվող շարժումներ կատարել` պարբերաբար անցնելով հավասարակշռության դիրքով։
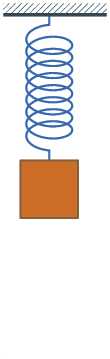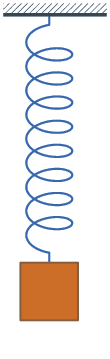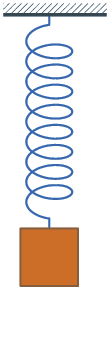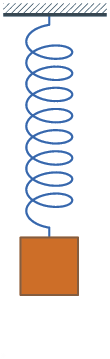
Զսպանակավոր ճոճանակը k կոշտությամբ անկշիռ զսպանակից կախված m զանգվածով բեռ է և ի վիճակի է տատանվել զսպանակի առաձգականության ուժի շնորհիվ։
Մաթեմատիկական և զսպանակավոր ճոճանակների տատանումները, որոնք քննարկվել են նախորդ պարագրաֆներում, կոչվում են ազատ:
Ազատ տատանումները տեղի են ունենում «ինքնաբերաբար», առանց արտաքին, պարբերաբար փոփոխվող ուժերի ազդեցության:
Տատանումների գրաֆիկի ձևի մասին կարելի է դատել՝ կատարելով հետևյալ փորձը.
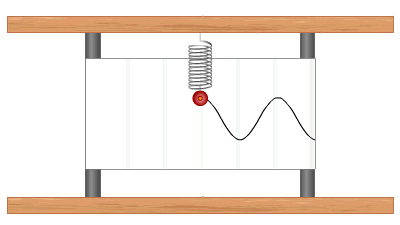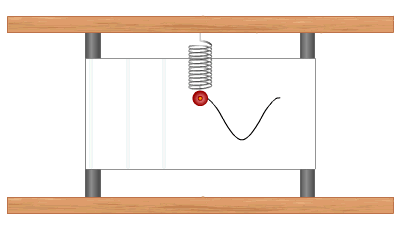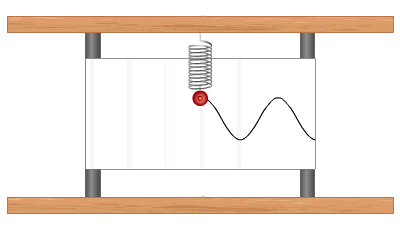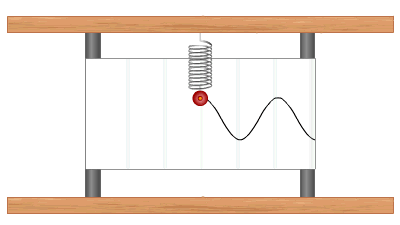
Այն տատանումները, որոնք կատարվում են համակարգում գործող ներքին ուժերի շնորհիվ, անվանում են ազատ տատանումներ:
Եթե ներքին ուժերի թվում կան նաև շփման կամ դիմադրության ուժեր, ապա տատանումների լայնույթն աստիճանաբար փոքրանում է:
Այն տատանումները, որոնց լայնույթն աստիճանաբար փոքրանում է, անվանում են մարող տատանումներ: Ազատ տատանումները շփման և դիմադրության ուժերի առկայությամբ մարող են լինում: Oրինակ, մաթեմատիկական ճոճանակում Երկրի ձգողության ուժը դանդաղեցնում է գնդիկին նրա բարձրանալու ժամանակ, բայց իջնելիս արագացնում է: Հարկ է նշել, որ շփման ուժը ոչ միայն բարձրանալիս է դանդաղեցնում գնդիկի շարժումը, այլ նաև իջնելիս:
Դիմադրության և շփման ուժերը միշտ գոյություն ունեն: Չմարող, այսինքն այնպիսի տատանումներ, որոնց լայնույթն աստիճանաբար չփոքրանա ստանալու համար, պետք է որ համակարգի վրա ազդի պարբերաբար փոխազդող ուժ:
Այն տատանումները, որոնք կատարվում են արտաքին պարբերաբար փոփոխվող ուժի առկայությամբ, անվանում են հարկադրական տատանումներ: Մաթեմատիկական (կամ զսպանակավոր) ճոճանակի տատանումներն օդի դիմադրության պատճառով մարող բնույթ են կրում. դրանց լայնույթն աստիճանաբար նվազում է, և, ի վերջո, ճոճանակը կանգ է առնում: Սակայն, եթե օդի դիմադրությունը փոքր է, ապա փոքր ժամանակահատվածներում այն կարելի է հաշվի չառնել: Այս դեպքում ճոճանակի նկատմամբ կարելի է կիրառել էներգիայի պահպանման օրենքը:
Օրինակ
Երբ մաթեմատիկական ճոճանակը հանում են հավասարակշռության վիճակից, այդպիսով նրան հաղորդում են որոշակի E պոտենցիալ էներգիա: Երբ ճոճանակը, թափ առնելով շրջանի աղեղով, սրընթաց ցած է իջնում (դեպի հավասարակշռության դիրքը), նրա պոտենցիալ էներգիան նվազում է, իսկ կինետիկը` աճում: Միջին դիրքում E կինետիկ էներգիան առավելագույնն է, իսկ պոտենցիալը` նվազագույնը (հավասար է զրոյի):
Օրինակ
Այն բանից հետո, երբ ճոճանակը իներցիայով շարունակի հեռանալ հավասարակշռության դիրքից, նրա կինետիկ էներգիան կսկսի նվազել, իսկ պոտենցիալը` աճել: Եզրային դիրքում ճոճանակի պոտենցիալ էներգիան կհասնի իր առավելագույն արժեքին, իսկ կինետիկ էներգիան կվերածվի զրոյի: Այնուհետև այս ամենը կկրկնվի հակառակ հաջորդականությամբ: Այսինքն, տատանումների ընթացքում նրա պոտենցիալ էներգիան պարբերաբար փոխակերպվում է կինետիկ էներգիայի, իսկ կինետիկ էներգիան` պոտենցիալի. Eպ→Eկ→Eպ→Eկ…
Ուշադրություն
Այս էներգիաներից յուրաքանչյուրն առանձին-առանձին փոփոխվում է, սակայն դրանց գումարը (այսինքն` \(E լրիվ)\ մեխանիկական էներգիան) շփման և դիմադրության ուժերի բացակայության դեպքում մնում է անփոփոխ:
Այդ ուժերի առկայությամբ պոտենցիալ և կինետիկ էներգիաների հաջորդական փոխակերպումներից ամեն մեկի ընթացքում լրիվ մեխանիկական էներգիայի որոշ կորուստ է լինում: